Recibido para Arbitraje: 03/03/2016
Aceptado para Publicación:07/07/2016
Los estudios paramétricos parten del supuesto que vienen de una distribución normal, por el contrario, los métodos no paramétricos son la manera más directa de solucionar el problema de falta de normalidad. El estudio tuvo como objetivo comparar los estudios paramétricos con los estudios no paramétricos y sus aplicaciones en la investigación odontológica. El estudio fue de tipo descriptivo documental, con diseño bibliográfico, para la técnica de recolección de datos se utilizó la observación directa a fuentes documentales, se realizó una revisión sistemática de artículos científicos referentes a la estadística y al área odontológica. Se concluyó que la aplicación de las diversas pruebas paramétricas y no paramétricas va a depender de las características de la variable objeto de estudio, el tamaño de la muestra y de la escala de medición de los datos. Así mismo, el investigador de la odontología va a disponer de aplicaciones específicas para estudiar las variaciones de los grupos de estudios y con ello tener la suficiente evidencia estadística en la toma de decisiones clínicas aportando con ello estudios confiables.
Palabras clave: Estadística inferencial, pruebas estadísticas, odontología.
Parametric studies are based on the assumption that they come from a normal distribution, on the contrary, non-parametric methods are the most direct way to solve the problem of lack of normality. The study aimed to compare parametric studies with non-parametric studies and their applications in dental research. The study was descriptive documentary, with a bibliographic design, for the data collection technique was used direct observation to documentary sources, a systematic review of scientific articles concerning statistics and the dental area. It was concluded that the application of the various parametric and non-parametric tests will depend on the characteristics of the variable object of study, the sample size and the measurement scale of the data. Likewise, the dentistry researcher will have specific applications to study the variations of the study groups and thus have sufficient statistical evidence in clinical decision making, thus providing reliable studies.
Key words: Inferential statistics, statistical tests, dentistry.
Los estudios orientados al área odontológica en los últimos años han demostrado una presencia significativa en el campo de la investigación, con el propósito de informar a las personas de los últimos avances en materia de salud bucal, lógicamente esas investigaciones tienen un componente estadístico el cual va a permitir arrojar resultados cuantitativos y/o cualitativos confiables y precisos acerca del comportamiento de determinada enfermedad, evento o factor.
La estadística es hoy una de las herramientas más útiles e influyentes en la mayoría de los campos del conocimiento, ya que ofrece un abanico de posibilidades de aplicación, y más aun si se considera la velocidad con la que se genera el desarrollo tecnológico, el volúmen de nueva información y el avance vertiginoso de la ciencia. Es un hecho que a lo largo del tiempo cada vez más disciplinas encuentran en los métodos estadísticos una opción para el adecuado planteamiento y solución de problemas específicos 1,2. Es por ello que obtener evidencias de la práctica odontológica para analizarla implica una serie de tareas y el desarrollo de habilidades para las cuales el común de los profesionales de la salud no está formado y que, en consecuencia, representan retos por vencer 3.
Todo profesional perteneciente al sector de la salud requieren de información cuantificada y resumida para tomar decisiones, por ejemplo, el envejecimiento progresivo de la población, los cambios de expectativas de las personas respecto de su propia salud y los cuidados a los que pueden acceder, los cambios en los patrones de morbilidad originados por nuevos hábitos, conductas y/o exposiciones de riesgo, entre muchos otros factores, condicionan la necesidad creciente de disponer de información que, a su vez, sea precisa, fiable y actualizada, sobre la cual fundamentar mejor las decisiones clínicas y sanitarias 4, 5.
Una de las técnicas estadísticas con mayor pertinencia en el campo de la investigación en odontología es el uso de las pruebas paramétricas y no paramétricas, por tener la capacidad de un mayor alcance y exactitud, a través de sus diversos estadísticos al abordar las variables de acuerdo a sus características y escalas de medición por medio de las cuales se conoce el grado de variación de una determinada patología bucal en un grupo de sujetos 6.
En otro orden de ideas, la inferencia estadística (estimaciones y contrastes de hipótesis) abarca el estudio de las características desconocidas de la población que resultan ser parámetros de la distribución de la población, de esa manera, a partir de las distribuciones muestrales se pueden diseñar métodos para estimar y contrastar los valores de los parámetros, según la distribución de la población de la que se trata. Sin embrago, la inferencia estadística no solo estudia el tratamiento de los datos de parámetros poblacionales sino que considera otras condiciones, tales como:
Por lo tanto, aunque aparentemente la estadística parece una ciencia fundamentalmente teórica, es utilizada en la odontología a diario; por ejemplo, cuando se medica algún fármaco reconocido al tratar determinada enfermedad, previamente para su recomendación se hizo uso de la estadística 7.
Por lo anteriormente señalado, se hace necesario comparar las pruebas paramétricas o no paramétricas y su aplicación en la investigación odontológica, permitiendo con ello contrastar, de acuerdo a la teoría de la estadística inferencial, la utilización de métodos adecuados que permitan medir las variables propias del área de salud bucal en un momento determinado.
La investigación fue de tipo descriptiva documental, con diseño bibliográfico. Para la técnica de recolección de la información se utilizó la observación directa a fuentes documentales especializada en la salud odontológica. El estudio fue el resultado de una revisión sistemática de diecisiete artículos científicos publicados en revistas arbitradas e indexadas en el área de la estadística y salud odontológica. Así mismo, se tomó como muestra siete publicaciones que cumplieron el criterio de inclusión el haber utilizado como método estadístico las pruebas paramétricas o no paramétricas para hacer su posterior comparación.
Cuando la estadística se basa en el conocimiento de las distribuciones muestrales por medio de diferencias de porcentajes o promedios, así mismo, cuando las muestras provienen de una misma población, se acepta entonces usar la aproximación normal, la distribución de t de Student o la distribución F de Fisher en el análisis de varianza, bajo el supuesto de que la hipótesis nula es cierta. Dado que en esos métodos se estiman los parámetros de las poblaciones de origen, esas técnicas estadísticas reciben el nombre de paramétricas 8.
Por el contrario, hay estudios en que, por el escaso número de observaciones, o por el nivel de medición de las variables, no es correcto o no es posible hacer supuestos sobre las distribuciones muestrales subyacentes, en tales casos se usan los métodos no paramétricos o de distribución libre.

Como se observa en la tabla I se expresa la comparación entre los métodos paramétricos y no paramétricos. En la estadística paramétrica, por medio de la cual el investigador aspira encontrar en las características de la muestra que ha seleccionado, aquellas que distinguen a la población de donde ésta procede, hay dos formas de actuar:
Se considera la aplicación de métodos paramétricos cuando las muestras son de gran tamaño (al menos un grupo mayor a 20 sujetos o unidades de información), al mismo tiempo, estas pruebas se aplican en determinadas variables que obedecen al tipo nominal o de intervalo, de igual manera, parten del supuesto que vienen de una distribución normal y las hipótesis se basan en valores provenientes de las medias y no considera los valores perdidos en su cálculo 8.
Por el contrario, los métodos no paramétricos son la manera más directa de solucionar el problema de falta de normalidad. Estos métodos son muy simples de usar y están disponibles en cualquier programa estadístico. Pero tienen dos desventajas: Primero, tienen menos poder que las equivalentes soluciones paramétricas y segundo, las pruebas de hipótesis no paramétricas no contestan a la misma pregunta que las pruebas paramétricas 8.
Los estudios no paramétricos son aplicables a grupos pequeños (muestras menos a 20), a variables de tipo categóricas y parten del supuesto de que se desconoce cómo están distribuidos los datos, las hipótesis se basan en rangos, medianas o frecuencia de datos y asumen los valores perdidos para su cálculo.
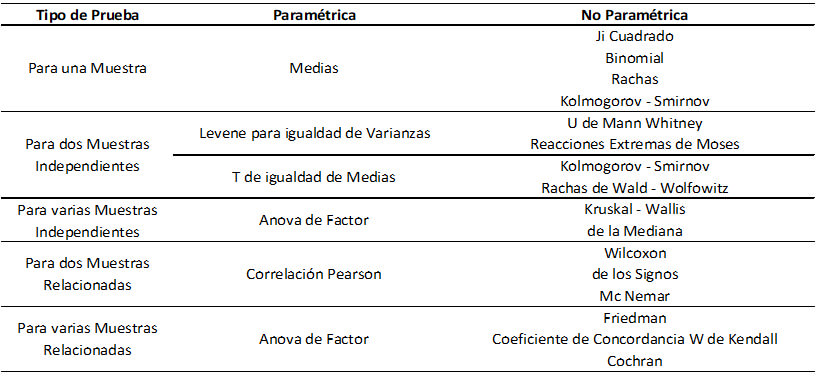
En la tabla II se comparan las aplicaciones estadísticas para estudios paramétricos y no paramétricos. Cuando se tiene solo una muestra y se desea conocer su comportamiento ante determinado fenómeno; es decir sólo se tiene una muestra de sujetos, y se requiere saber si dicha muestra difiere en los valores de la variable de los de una población u otra muestra de referencia; en el caso paramétrico la prueba idónea es para Una muestra a través de la prueba de la media. Para el caso de los estudios no paramétricos, aplica las pruebas Ji cuadrado, Binomial, de las Rachas y Kolgomorov – Smirnov.
En el caso que se pretenda probar una hipótesis respecto a uno o más parámetros de una población que tiende a una distribución normal, las pruebas usadas son las de la estadística paramétrica, como la t de Student para dos muestras independientes o dos muestras relacionadas; si es el caso para varias muestras independientes o relacionadas se utiliza Anova de un Factor.
Para los estudios no paramétricos se dispone de pruebas más específicas; tales como: para dos Muestras Independientes (U de Mann Whitney, Reacciones Extremas de Moses, Kolmogorov - Smirnov y Rachas de Wald – Wolfowitz), para varias Muestras Independientes (Kruskal – Wallis y de la Mediana) dos Muestras Relacionadas (Wilcoxon, de los Signos y Mc. Nemar), prueba para varias muestras relacionadas (Friedman, Coeficiente de Concordancia W de Kendall y Cochran)
Un poder estadístico inadecuado es quizá la causa más común de ensayos clínicos negativos. Para calcular el tamaño de una muestra para un estudio se tiene que especificar el efecto del tamaño, el nivel del significado estadístico y el poder deseado. Aunque el número de errores potenciales en medicina clínica es casi ilimitado, en la investigación clínica solamente pueden ocurrir dos errores básicos: encontrar una diferencia cuando realmente no existe (un error falso-positivo o error tipo I) y viceversa (un error falso-negativo o error tipo II). El error falso-positivo habitualmente es medido con la letra α, que usualmente se fija en 0.05 (el valor de p tradicional). Esto significa que los investigadores están dispuestos a aceptar una posibilidad de 1 en 20 de cometer este error. La conclusión falsa-negativa, por su lado, es medida con β, que habitualmente se fija más alto, por ejemplo 0.10 o 0.20. Esto significa que los investigadores están dispuestos a aceptar una posibilidad de 10 o 20 % de decir que no existe diferencia, cuando en realidad existe una deferencia en la población 9.
El poder de un estudio es su capacidad para evitar un error tipo II; matemáticamente, “poder” es igual a 1 – β. Una descripción verbal sería que “poder” es la capacidad de un estudio para encontrar una diferencia (estadísticamente significativa con un valor de p < α) si existe en la población. Por ejemplo, con un poder de 80 % y α de 0.05, un estudio tendría una posibilidad de 80 % de encontrar una diferencia estadísticamente significativa (en p < 0.05) si existe la diferencia en la población 9.
A tales consideraciones, el error de tipo I también denominado error de tipo alfa (α) o falso positivo, es el error que se comete cuando el investigador no acepta la hipótesis nula siendo ésta verdadera en la población. Es equivalente a encontrar un resultado falso positivo, porque el investigador llega a la conclusión de que existe una diferencia entre las hipótesis cuando en realidad no existe. Se relaciona con el nivel de significancia estadística 9.
El error de tipo II también llamado error de tipo beta (β) o falso negativo, es el error que se comete cuando el investigador no rechaza la hipótesis nula siendo ésta falsa en la población. Es equivalente a la probabilidad de un resultado falso negativo, ya que el investigador llega a la conclusión de que ha sido incapaz de encontrar una diferencia que existe en la realidad 9.
Contrariamente al error tipo I, en la mayoría de los casos no es posible calcular la probabilidad del error tipo II. La razón de esto se encuentra en la manera en que se formulan las hipótesis en una prueba estadística. Mientras que la hipótesis nula representa siempre una afirmación enérgica. Los errores tipo I y tipo II están relacionados. Una disminución en la probabilidad de uno por lo general tiene como resultado un aumento en la probabilidad del otro 9.
Al comparar los estudios paramétricos con los estudios no paramétricos y sus aplicaciones en la investigación odontológica, se seleccionaron siete artículos publicados considerando el uso de pruebas paramétrica o no paramétricas, según el caso:
El estudio tuvo como objetivo determinar la influencia del factor racial en la maduración ósea de niños escolares pertenecientes a las etnias Wayúu y Criolla, residentes en Maracaibo, Estado Zulia, Venezuela. La muestra estuvo conformada por Para ello se comparó las edades óseas estimadas entre las dos etnias, utilizando la estadística paramétrica prueba T para muestras independientes, las cuales permitieron contrastar hipótesis, referidas a la diferencia entre dos medias.
Para decidir si se pudo o no asumir que las varianzas poblacionales son iguales, el procedimiento prueba T para muestra independientes ofreció la prueba de Levene, la cual se aplicó para contrastar supuestos de homogeneidad de varianzas. Por otra parte, para verificar la relación entre las edades óseas estimadas y las edades cronológicas, se utilizó el coeficiente de correlación de Pearson 10.
La investigación estuvo orientada a demostrar la reproductibilidad intraobservador en la estimación de la edad ósea, a través del método Tanner-Whitehouse 3 (TW3), en una población de escolares residentes en Maracaibo, estado Zulia, Venezuela. En el cual se aplicó la estadística paramétrica (prueba t para muestras relacionadas o datos apareados), comparando los resultados de la estimación de la edad ósea y para verificar la relación en ambas evaluaciones se aplicó el coeficiente de correlación de Pearson 11.
El estudio estuvo dirigido a evaluar el estado de salud gingival de adolescentes con y sin ortodoncia, comparando sus parámetros periodontales, utilizando la prueba Kolmogorov- Smirnov para verificar la distribución normal de las variables continuas. Los datos categóricos se analizaron con pruebas de X2; las comparaciones entre los dos grupos se realizaron con la prueba de U de Mann–Whitney debido a que los datos no siguieron una distribución normal 12.
El objetivo del estudio fue evaluar los tratamientos periodontales sencillos realizados por los estudiantes a sus pacientes, considerando como métodos estadísticos lo no paramétricos: Prueba de Wilcoxon para comparar el Índice Periodontal (I.P) y el Índice de Higiene Oral Simplificado (IHOS) antes y después del tratamiento. Prueba de U de Mann - Whitney para encontrar diferencias entre los valores finales del Índice Periodontal (IP) e Índice de Higiene Oral Simplificado (IHOS) con la variable nivel clínico del estudiante 13.
El estudio tuvo como objetivo evaluar comparativamente los alcances terapéuticos entre el tratamiento odontológico convencional y el uso combinado de éste, con la fisioterapia y la osteopatía, aplicados en pacientes que acudieron con Disfunción Temporomandibular, para ello tomó como método estadístico el análisis inferencial, al contrastar las dos hipótesis generales, la variable dolor medida con la prueba de Kolmogorov-Smirnov y la variable apertura bucal mediante la t de Student 14.
La investigación tuvo como objetivo determinar el lado de preferencia masticatoria en niños con fisura palatina, las comparaciones entre los pacientes con preferencia masticatoria derecha e izquierda, se realizaron con la prueba U de Mann-Withney. Para el análisis de varianza de las medidas cuantitativas entre los pacientes con tres tipos de fisura, se utilizó la prueba H de Kruskall-Wallis y, posteriormente, se realizaron las comparaciones con la prueba U de Mann-Withney 15.
El objetivo del estudio fue analizar la prevalencia de accidentes de trabajo entre los docentes de la facultad de odontología de la Universidad Federal de Espíritu Santo, Brasil Noveno semestre de 2010/1. Tomando como método estadístico el Ji cuadrado para verificar en nivel de asociación entre las variable 16.
De los casos expuestos en el presente trabajo, se encontraron cinco artículos que utilizaron en su análisis estadístico pruebas no paramétricas, así como también, se identificaron dos manuscritos cuya herramienta fueron las pruebas paramétricas, considerando en todos los casos, las siguientes condiciones: las características de la variable a estudiar y el objetivo del mismo.
EL resultado se soporta en el basamento teórico acerca de las pruebas no paramétricas, las cales engloban una serie de pruebas estadísticas que tienen como denominador común la ausencia de asunciones acerca de la ley de probabilidad que sigue la población de la que ha sido extraída la muestra. Por esta razón es común referirse a ellas como pruebas de distribución libre 17.
Al mismo tiempo, los estudios paramétricos son comunes cuando se pretende probar una hipótesis respecto a uno o más parámetros de una población que tiende a una distribución normal. Por otra parte, al estudiar una o varias muestras siendo menores a 11 casos, la potencia estadística de las pruebas paramétricas y no paramétricas es similar; a medida que aumenta el tamaño de las muestras las pruebas paramétricas aumentan su potencia, por lo que las pruebas no paramétricas están indicadas cuando la muestra sea menor de once o bien cuando hay una muestra mayor pero no se cumplen los requisitos de aplicabilidad de las pruebas paramétricas 8.
Se concluye que la aplicación de las diversas pruebas paramétricas y no paramétricas va a depender de las características de la variable objeto de estudio, el tamaño de la muestra y de la escala de medición de los datos. Así mismo, el investigador de la odontología va a disponer de aplicaciones específicas para estudiar las variaciones de los grupos de estudios y con ello tener la suficiente evidencia estadística en la toma de decisiones clínicas aportando con ello estudios confiables.
En ese sentido, las pruebas no paramétricas son más exigentes al rechazar la hipótesis nula de igualdad y por tanto tienen menos posibilidades de acertar cuando no la rechazan (más posibilidades de cometer un error tipo beta).
A tales consideraciones, es recomendable, al abordar estudios orientados a la investigación odontológica, disponer de un tamaño de muestra lo suficientemente grande para tener mayor probabilidad de encontrar una diferencia verdadera entre los grupos de estudio (poder estadístico).